|
[J12][.pdf
.bib]
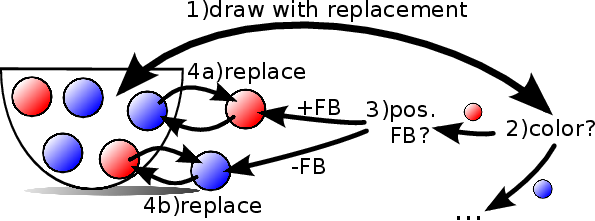
Heiko Hamann Towards Swarm Calculus: Urn Models of Collective Decisions and Universal Properties of Swarm Performance Swarm Intelligence, 7(2-3):145-172, 2013 |
|
[C26][.pdf
.bib
cited by] Heiko Hamann Towards Swarm Calculus: Universal Properties of Swarm Performance and Collective Decisions ANTS 2012, Brussels, Belgium, Marco Dorigo et al. (eds.), LNCS 7461, pp. 168-179, Springer-Verlag, 2012 |